在本文中，我们将讨论一种不同的非理想情况：转换速率，它定义为运算放大器的输出电路可以产生的电压变化率。如果理论输出波形的斜率超过转换速率，则实际输出波形将偏离输入波形的形状，如图 1 所示。

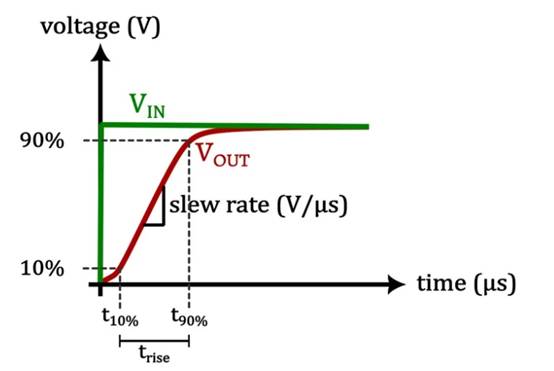
图 1.运算放大器输出的压摆率限制，上升时间由trise表示。图片由罗伯特·凯姆提供压摆率通常以伏特每微秒 (V/μs) 为单位。如果我们将转换速率乘以一段时间，结果就会告诉我们输出电压在这段时间内会增加多少。然而，更常见的是，我们使用运算放大器的指定转换速率来估计上升时间，或者相反，估计下降时间。

我们可以将上升时间（上图中的 trise）定义为信号从其新值的 10% 增加到 90% 所需的时间。下降信号的转换率类似，的区别是我们现在测量从 90% 下降到 10% 的变化。请注意，本文的其余部分将仅讨论上升输出信号的转换速率限制。

为了估计上升时间，我们将 80% 的预期输出变化除以压摆率。这种测量上升时间的方法减少了上升沿开始或结束时发生的逐渐变化的影响。通过看一个例子我们可以更好地理解这一点。

上升时间：一个例子

假设我们需要一个运算放大器来放大传入的传感器信号，当某个物理事件发生时，该信号将从 0 V 快速转换到 500 mV。我们将假设以下情况：

我们将运算放大器配置为增益为 10 的同相放大器，以便预期输出从 0V 快速转变为 5V。

我们使用经典的 741 运算放大器，其转换速率约为 0.5 V/μs。

在这种情况下，10% 到 90% 的条件对应于从 0.5 V 增加到 4.5 V，电压增加了 4 V。上升时间计算如下：

t上升 = 4 V0.5 Vμs = 8 μ文字s

接下来，我们将使用图 2 中的 LTspice 原理图通过仿真来确认上升时间。

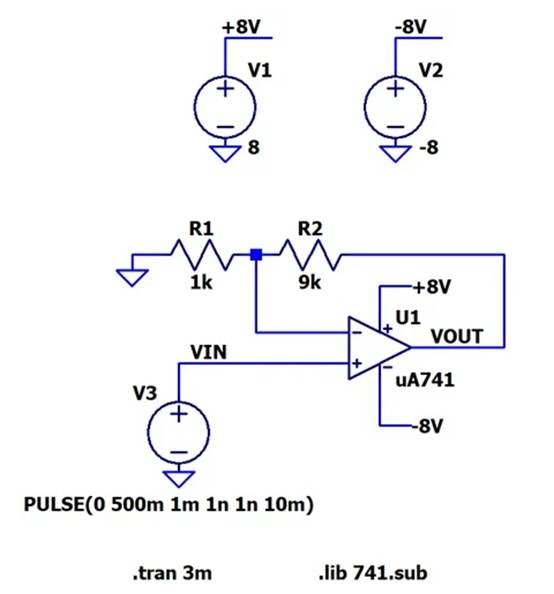
图 2.用于测试 741 运算放大器压摆率的 LTspice 电路。图片由罗伯特·凯姆提供图 3 显示了仿真结果。正如您所看到的，运算放大器的输出信号的上升速度不如输入信号的急剧上升。

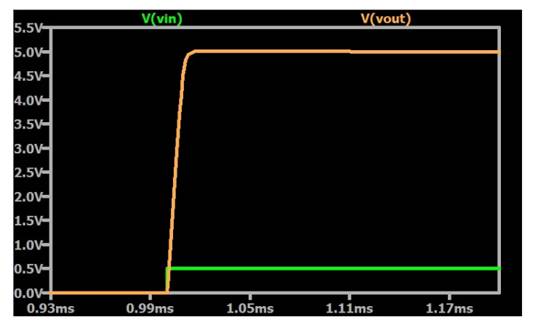
图 3. 模拟阶跃函数输入和转换速率限制输出。图片由罗伯特·凯姆提供我们可以通过放大并使用光标功能来测量上升时间和转换速率（图 4）。

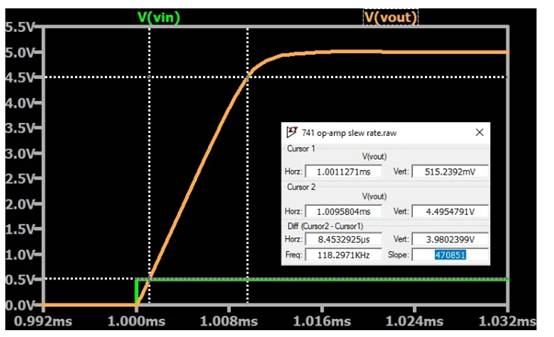
图 4. LTspice 的光标功能使我们能够测量输出斜坡的斜率。图片由罗伯特·凯姆提供从V OUT = 0.5 V 到V OUT = 4.5 V的输出信号看起来非常线性。上升时间约为 8.5 μs，接近我们的理论值。波形这部分期间的斜率为 470,851 V/s，约为 0.47 V/μs。这表明仿真中使用的 SPICE 模型成功地再现了预期的约 0.5 V/μs 的 741 转换速率。

转换速率对正弦信号的影响

我们现在已经了解了运算放大器的压摆率如何增加输出波形的上升时间，从而导致快速输入阶跃转换变为线性斜坡输出转换。然而，转换速率限制不仅影响阶跃函数。它们会影响任何需要比运算放大器支持的变化速度更快的输出信号，例如高频正弦信号。

对于正弦信号，我们主要考虑非线性导致的失真。如果实际输出信号的上升速度不能与预期输出信号的较高斜率部分一样快，则运算放大器将无法维持输入和输出之间的线性关系。

图 5 显示了转换速率引起的失真的一个极端示例。输出的上升沿和下降沿受到转换速率的限制。结果，信号现在是三角波而不是正弦波。

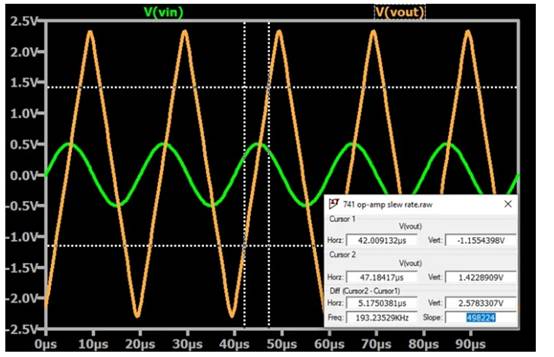
图 5.模拟 741 运算放大器在正弦曲线的较高斜率部分期间遇到转换速率限制。图片由罗伯特·凯姆提供是什么导致转换速率限制？

电路中的延迟和带宽限制从根本上来说是由电容引起的。电流在电路内流动并通过阻抗时产生电压。然而，电压不会立即出现——电流必须首先对寄生电容和有意电容进行充电或放电。较大的电容需要更多的充电电流并导致更长的延迟。

运算放大器具有必须充电和放电的内部电容，这些电容限制了输出电压变化的速率。在许多情况下，这些内部电容包括相对较大的补偿电容器。

例如，图 6 显示了Texas Instruments 的LM124运算放大器的内部原理图。其补偿电容器 ( CC )降低了放大器第二级中电压变化的速率。

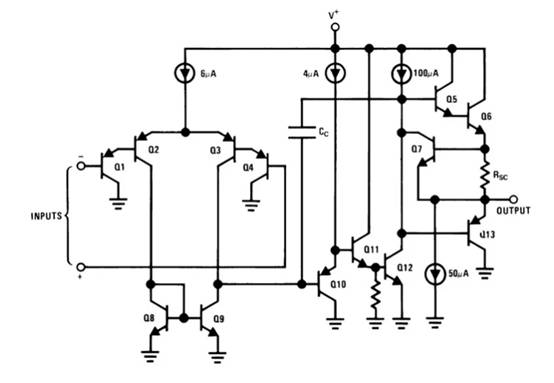
德州仪器 (TI) LM124 运算放大器的内部原理图。

图 6. LM124 运算放大器的内部原理图。其补偿电容标记为C C 。图片由德州仪器 (TI)提供内部补偿电容器使运算放大器更加稳定，但会降低压摆率。非补偿运算放大器不使用补偿电容器，而是受到较小寄生电容的限制。因此，它们提供了更高的转换速率。